Bloomberg SWPM-OV vs a Transparent Request
Bloomberg is the reference on most desks. This page compares a SWPM-OV output with the same instrument priced from a fully explicit Quantra request.
Result at a glance
The goal is not to reverse-engineer every Bloomberg detail. The goal is to show that a pricing number only exists together with its assumptions — and if the assumptions are hidden, the number cannot truly be validated.
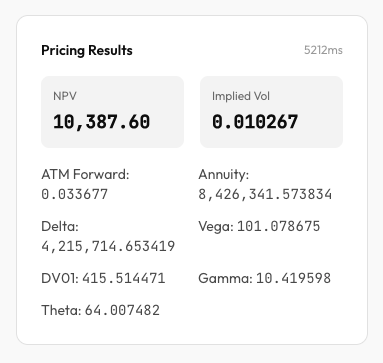
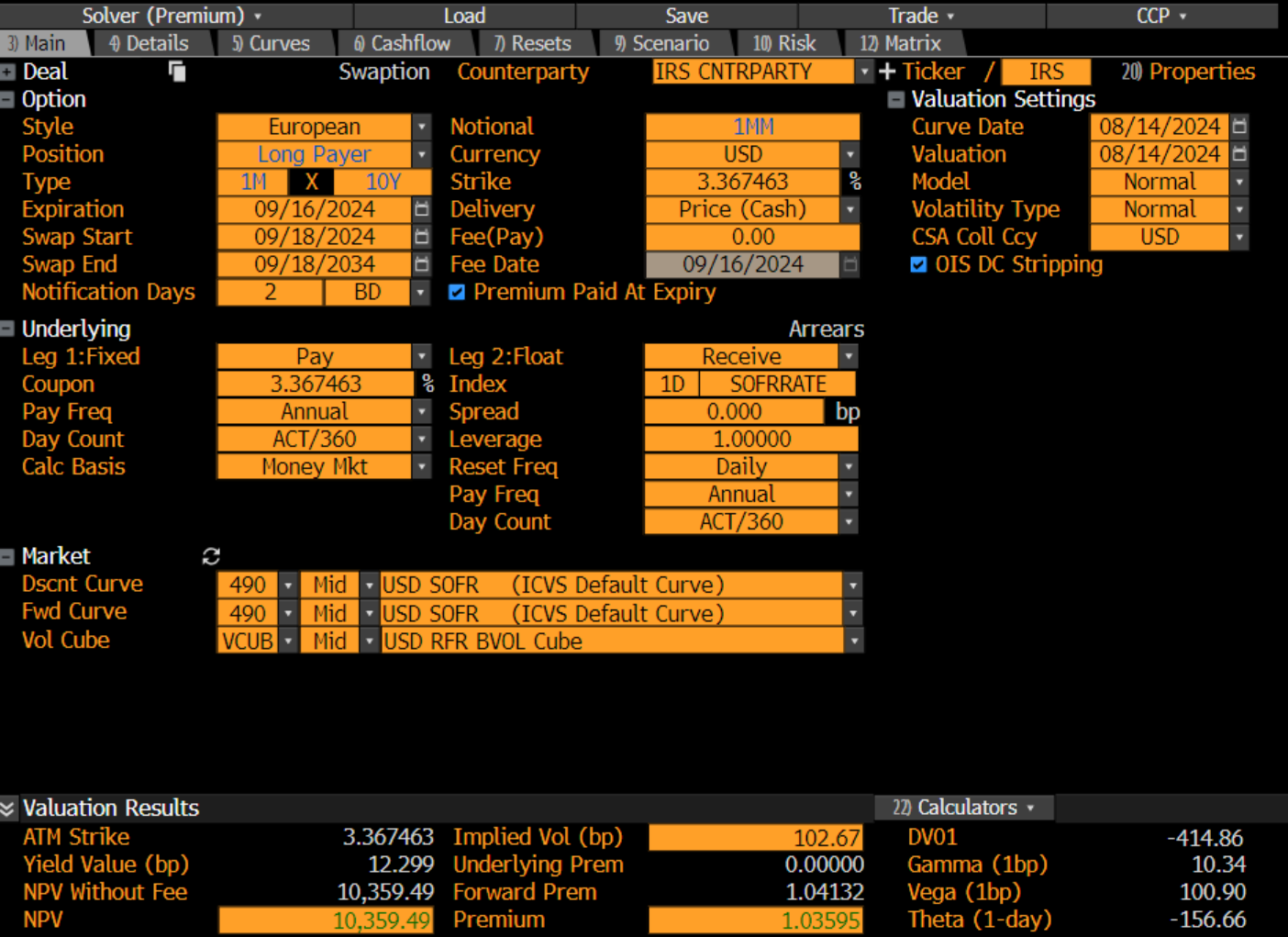
| Metric | Bloomberg | Quantra |
|---|---|---|
| Fair rate | 3.367463% | 3.3724% ATM forward |
| Premium (NPV) | 10,359.49 | 10,585.40 |
| DV01 (1bp) | -414.86 | 430.13 |
| Gamma (1bp) | 10.34 | 10.94 |
| Vega (1bp) | 100.90 | 101.07 |
| Theta (1d) definition | -156.66 | -131.55 |
Updated 2026-10-12. The Quantra column is what the linked JSON request returns on engine 0.8.2 (swaption_pricing_rebump: true), re-run against the public API. Premium, DV01, gamma and vega are unchanged from engine 0.7.0. Theta was missing on 0.7.0 for requests whose curve is an interpolated zero-rate curve (the one-day roll moved the evaluation date but not the curve's own reference date); engine 0.8.0 fixed this, the roll now moves every reference date, so theta includes the curve roll and the option's time decay. Bloomberg's theta definition is not published, which is the usual source of the gap in this row. An earlier version of this page showed numbers from a portal example run whose inputs were never published (NPV 10,387.60); they could not be reproduced from the linked request and were replaced.
Bloomberg values are shown for visual comparison and context.
Why matching Bloomberg is harder than it looks
A swaption price is not a formula. It is a model plus a curve, plus conventions, plus a definition for each greek.
- Curve construction: helpers, settlement days, calendars, and day count.
- Settlement conventions: cash-settled,
ParYieldCurvemethod. - Volatility convention: Normal (Bachelier) vs lognormal (Black).
- Greek definitions: DV01/Gamma/Vega/Theta are typically bump-and-reprice, not analytic model greeks.
Working assumption: to match SWPM-OV greeks you usually need to reproduce Bloomberg’s definitions, not just the pricing model.
Why theta usually diverges
Theta is the change in value after one day passes. That definition is ambiguous, so different systems can legitimately disagree. Quantra defines theta as npvTomorrow - npv with a one-day roll of the evaluation date and of every curve and volatility reference date (engine 0.8.0 and later); you can verify this in the source code here: swaption_pricing_request.cpp. You can check what we do; you cannot do that with Bloomberg.
- Frozen-curve theta: advance the evaluation date but keep the curve shape fixed (time decay only).
- Roll-down theta: rebuild the curve at
T+1using the same quotes, so time decay and roll-down both appear.
That is why theta is highlighted above: Bloomberg’s definition is implicit, while Quantra/QuantLib makes it explicit and reproducible.
DV01 sign conventions
DV01 can flip sign depending on whether the system applies the trade direction (payer vs receiver) or reports a raw rate-bump sensitivity. Bloomberg appears to apply a signed convention for this trade, while Quantra reports the direct bump-and-reprice change. That difference is visible in the table and is another example of why explicit definitions matter.
What Quantra does differently (and why it is a feature)
Quantra makes the request the contract. Curves, conventions, and model choice are explicit in JSON.
- Transparent inputs: every curve point, convention, and model choice is explicit.
- Reproducible results: requests are portable, versionable, and auditable.
- Controlled trade-offs: choose fast greeks or full rebump greeks depending on accuracy/performance needs.
Key settings to match Bloomberg
- Curve build: OISRateHelper with SOFR overnight index (annual fixed leg).
- Curve interpolation: BackwardFlat + ForwardRate bootstrap.
- Settlement: Cash, ParYieldCurve.
- Analytics:
swaption_pricing_rebump: true.
Bloomberg information (source)
Source post: quant.stackexchange.com/questions/80301/quantlib-swaption-pricing.
Local copies of the Bloomberg screenshots are available for offline viewing: image 1 (deal screen) and image 2 (Curve Data tab).
Where the market data in the request comes from
The 32 rates in the linked JSON (1 week to 50 years) are the table the Stack Exchange author posted as "copied from Bloomberg", not the values on the Curve Data screenshot. The two are different snapshots of curve 490: at every visible tenor the table sits 0.3 to 1.5bp below the screen's Market Rate column. The request feeds those 32 numbers as continuously compounded zero rates. Read instead as SOFR OIS par rates and bootstrapped, the same numbers give an NPV of about 9,730 and a forward of 3.352%; read as zero rates they give 10,585.40 and a forward of 3.372%; Bloomberg's own forward, 3.367463%, sits between the two. The forward is the whole difference: repricing with the strike set at the engine's own ATM gives 10,382, within 0.2% of Bloomberg's 10,359.49. An independent QuantLib reproduction in the same thread, reading the table as par rates, reports 9,745.84.
Reproduce these results
To reproduce the numbers above, either:
- Send this JSON request to the API: swaption_ois_bbg_zerorate_request.json.
- Or paste the 32 rates from the source post into the Quantra MCP server (mcp.quantra.io) from Claude and ask it to price the trade; it bootstraps the curve, prices, and can reprice under either reading of the rates.
Conclusion
Bloomberg is extremely useful because it is consistent. Open implementations are useful because they are explainable. The product advantage is being able to make definitions explicit, reproducible, and auditable.
This article mentions Bloomberg for comparative and educational purposes. Trademarks belong to their respective owners.